IDAF Vektoren in der Ebene
-Inhalt-
Darstellung von Vektoren in der Ebene ▶
Orts- und freie Vektoren ▶
Betrag eines Vektors in der Ebene ▶
Addition von Vektoren ▶
Polarkoordinaten ▶
Aufgaben inkl. Lösungen ▶
Physik Pilotaufgaben ▶
Darstellung von Vektoren in der Ebene
Vektoren sind Objekte, welche einen Betrag und einen Richtungssinn haben. Sie können als Pfeile dargestellt werden. Dabei ist die Länge des Pfeils der Betrag und die Pfeilspitze der Richtungssinn. In der Formelschreibweise werden Vektoren mit kleinen lateinischen Buchstaben bezeichnet und durch einen Pfeil über der Vektorgröße markiert. Vektoren können auch durch den Anfangspunkt und Endpunkt beschrieben werden, dabei wird der Anfangspunkt und der Enpunkt nacheinader notiert und durch einen Pfeil über den Buchstaben markiert.
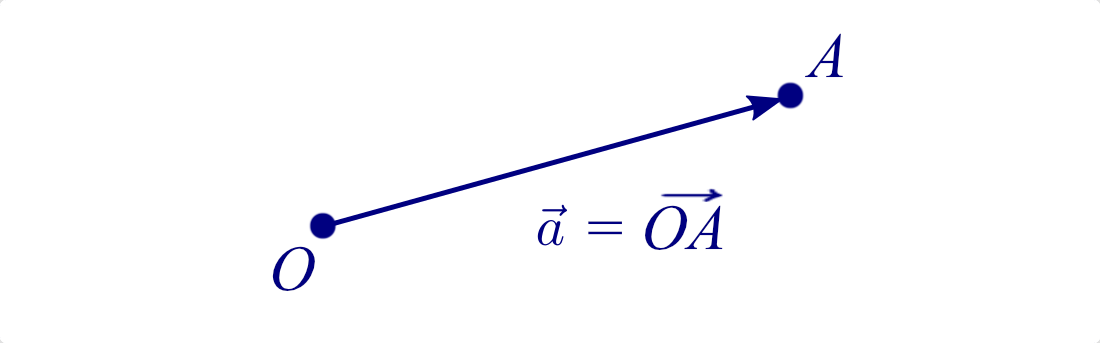
Übung 01:
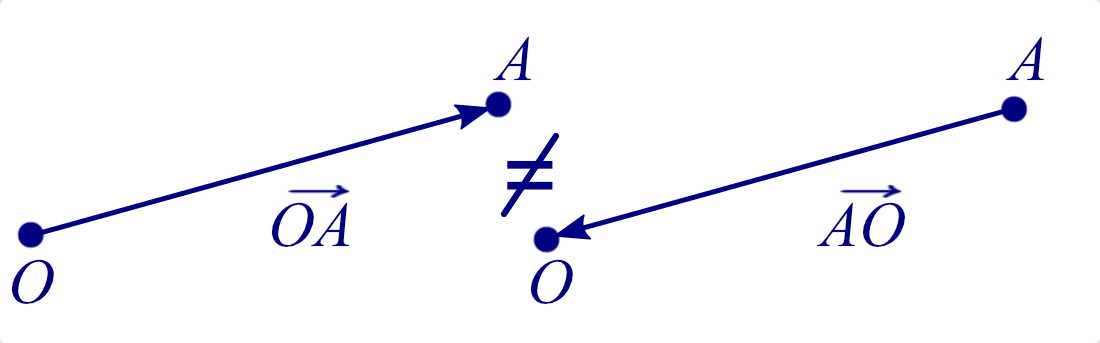
Ist der Vektor \( \overrightarrow{OA} \) gleich dem Vektor \( \overrightarrow{AO} \)
Lösung
Nein, da die Vektoren entgegengerichtete sind.
Ein Vektor wird in einem kartesischen Koordinatensystem durch seine Komponeten in der Komponentenschreibweise beschrieben. Die Komponenten sind dabei die x-Werte bzw. y-Werte im kartesischen Koordinatensystem.
Dabei liegt der Anfangspunkt des Vektors (in Bsp. unten O) beim Ursprung und der Endpunkt (in Bsp. unten A) beliebig.
Um den Vektor von einem Punkt zu unterscheiden,
werden die Vektoren mit einem Tupel beschrieben. Das ist eine grosse, runde Klammer, in der die Komponenten übereinander geschrieben werden. Oben liegt immer die x-Komponenten
und unten die y-Komponente. Mit der Komponentenschreibweise kann man alle Vektoren eindeutig beschreiben.
Probieren Sie es selber und verschieben Sie den Punkt A und beobachten Sie was mit den Komponenten geschieht.
Orts- und freie Vektoren
Ein Ortsvektor hat den Anfangspunkt immer im Ursprung des Koordinatensystems. Jeder Punkt einer Ebene kann durch einen Ortsvektor
beschrieben werden. Der Ortsvektor ist jedoch kein Punkt, sondern ein Vektor der beim Ursprung startet und genau beim beschriebenen Punkt endet (siehe: oberes Beispiel).
Ein Vektor muss nicht im Ursprung des Koordinatensystems starten. Ein freier Vektor kann bei einem beliebigen Punkt auf der Ebene starten und darf frei verschoben werden,
solange man weder die Länge noch den Richtungssinn des Vektors verändert. Die Komponenten bleiben somit konstant und können mit folgender Formel berechnet werden:
Komponente der Koordinate = Endpunktkoordinate - Anfangspunktkoordinate
Beispiel (siehe unten): \( \vec{a}=\left(\begin{array}{c}3-1\\1-2\end{array}\right)=\left(\begin{array}{c}2\\-1\end{array}\right) \)
Verschieben Sie den freien Vektor \( \vec{a} \) und rechen Sie nach ob die Komponenten tatsächlich konstant bleiben.
Übung 02:
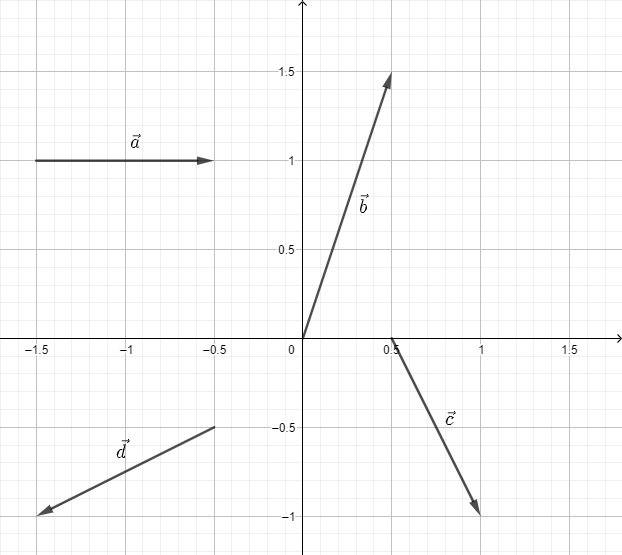
Berechnen Sie die Komponenten der Vektoren
\(
\vec{a}, \vec{b}, \vec{c}
\)
und
\(
\vec{d}
\)
und schreiben Sie sie mit einem Tupel.
Welche sind freie Vektoren?
Lösung
\[
\vec{a}=\left(\begin{array}{c}1\\0\end{array}\right), \ \vec{b}=\left(\begin{array}{c}0.5\\1.5\end{array}\right), \ \vec{c}=\left(\begin{array}{c}0.5\\-1\end{array}\right), \ \vec{d}=\left(\begin{array}{c}-1\\-0.5\end{array}\right)
\]
\(
\vec{a} \ , \ \vec{c} , \ \vec{d} \
\)
sind freie Vektoren.
\(
\vec{b} \
\)
kann ein Ortsvektor oder ein freier Vektor sein.
Um in Zukunft die Ortsvektoren von den freien Vektoren zu unterscheiden, beschreiben wir ein Ortsvektor mit \( \vec{r}. \) Um die Ortsvektoren untereinander zu unterscheiden, benutzen wir die Indexschreibweise: \[ \vec{r}_a \ne \vec{r}_b\ne \vec{r}_c \]
Übung 03:
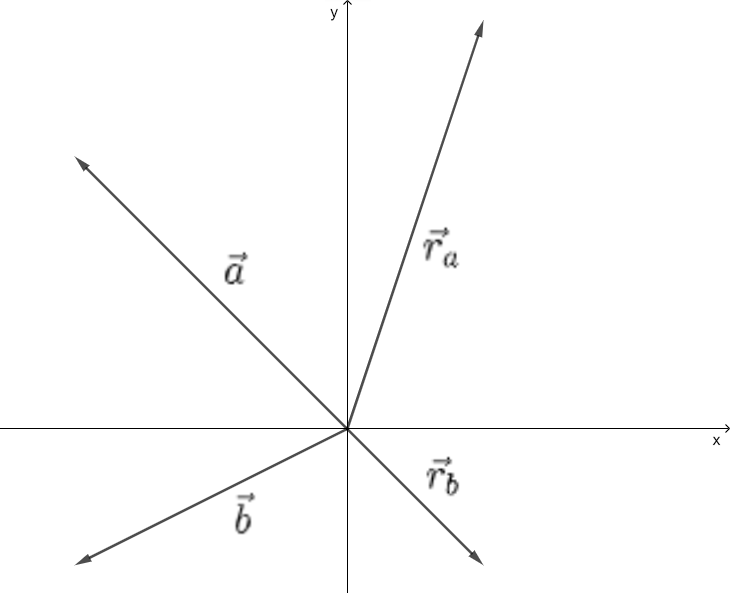
Welche dieser Vektoren sind Ortsvektoren?
Lösung
\( \vec{r}_a \ , \ \vec{r}_b \) sind Ortsvektoren.
Betrag eines Vektors in der Ebene
Die Strecke zwischen dem Anfangspunkt (O) und dem Endpunkt (A) eins Vektors wird Betrag genannt. Der Betrag wird mit zwei vertikalen Linien neben dem Vektor symbolisiert \( \overline{AB}=|\vec{a}|. \ \)
Übung 04:
Ist der Betrag des Vektors \( \overrightarrow{OA} \) gleich dem Betrag des Vektors \( \overrightarrow{AO} \ ? \)
Lösung
Ja, da die Strecken der beiden Vektoren gleich sind.

Der Betrag eines Vektors kann mit Hilfe des Satzes von Pythagoras anhand seiner beiden Komponenten berechnet werden:

\[ \overrightarrow{OA}=\vec{a}=\left(\begin{array}{c}x\\y\end{array}\right) \rightarrow \overline{OA}=|\vec{a}|=\sqrt{x^2+y^2} \]
Übung 05:
Berechnen Sie den Betrag der folgenden Vektoren: \[ \vec{a}=\left(\begin{array}{c}1\\1\end{array}\right), \ \vec{b}=\left(\begin{array}{c}3\\4\end{array}\right), \ \vec{c}=\left(\begin{array}{c}0\\-1\end{array}\right), \ \vec{d}=\left(\begin{array}{c}3\\-2\end{array}\right) \]
Lösung
\[ |\vec{a}|=\sqrt{2}, \ |\vec{b}|=5, \ |\vec{c}|=1, \ |\vec{d}|=\sqrt{13} \]
Addition von Vektoren
Ein freier Vektor kann durch Beibehalten seiner Länge und Richtung parallel auf der Ebene verschoben werden, ohne dass sich die Werte seiner
Komponenten ändern. Dies kann genutzt werden, um zwei Vektoren zeichnerisch zu addieren.
Fügt man an einen Vektor
\(
\vec{a}
\)
einen zweiten Vektor
\(
\vec{b}
\)
durch eine passende Verschiebung (Translation) so an, dass der Anfangspunkt des
zweiten Vektors mit dem Endpunkt des ersten Vektors übereinstimmt, dann erhält
man den Summenvektor
\(
\vec{c}=\vec{a}+\vec{b}
\)
, indem man den Anfangspunkt des ersten Vektors mit dem Endpunkt des zweiten Vektors verbindet.
Verschieben Sie wie oben beschrieben die Vektoren \( \vec{a} \) und \( \vec{b} \) bis Sie Vektor \( \vec{c} \) erhalten und prüfen Sie ihr Resultat.
Rechnerisch erhält man den Summenvektor, indem man die einzelnen Komponenten beider Vektoren addiert:
\( \vec{c}=\vec{a}+\vec{b}=\left(\begin{array}{c}a_x\\a_y\end{array}\right)+\left(\begin{array}{c}b_x\\b_y\end{array}\right)=\left(\begin{array}{c}a_x+b_x\\a_y+b_y\end{array}\right)=\left(\begin{array}{c}c_x\\c_y\end{array}\right) \)
Überprüfen Sie ob das gemäss der oberen Zeichnung stimmt.
Übung 09:
Addieren Sie die folgenden Vektoren: \[ \vec{a}=\left(\begin{array}{c}-5\\7\end{array}\right), \ \vec{b}=\left(\begin{array}{c}2\\-3\end{array}\right) \]
Lösung
\[ \vec{c}=\left(\begin{array}{c}-3\\4\end{array}\right) \]
Polarkoordinatendarstellung
Punkte können auch durch ihren Abstand zum Ursprung (Radius) und den Winkel zur positiven x-Achse (Polarwinkel) in einem Polarkoordinatensystem beschrieben werden.
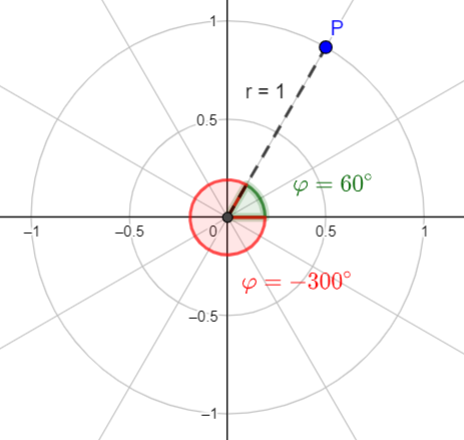
Diese Koordinaten des Punktes werden Polarkoordinaten genannt. Um die Polarkoordinaten von den kartesischen Koordinaten zu unterscheiden, verwendet man das Winkelzeichen:
\[ P(r\angle \varphi) \]Der Polarwinkel kann positiv im Gegenuhrzeigsinn oder negative im Uhrzeigersinn beschrieben werden. Üblicherweise nimmt man für den ersten und zweiten Quadranten den positiven Winkel und für den dritten und vierten Quadraten den negativen Winkel. Der Radius ist immer positiv.
Übung 06:
Zeichnen Sie die folgende Punkte auf ein Blattpapier: \[ P_1(1.5\angle45°), \ P_2(2\angle-120°), \] \[ \ P_3(1\angle-180°), \ P_4=(1\angle180°) \]
Lösung
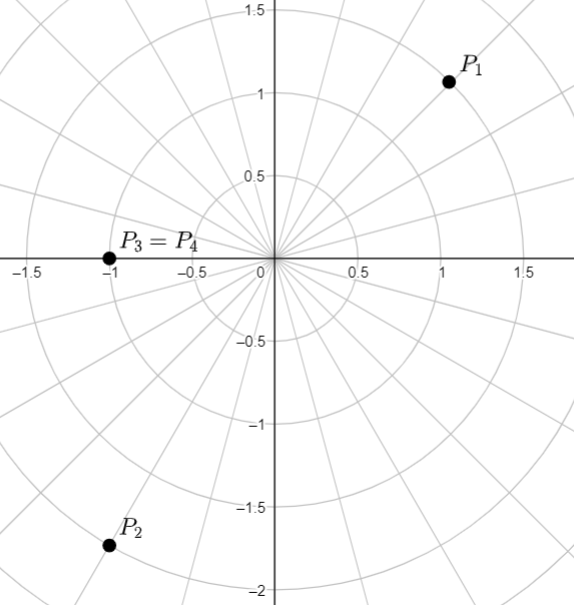
Die Polarkoordinaten müssen oft in kartesischen Koordinaten umgerechenet werden. Die beiden kartesische Koordinaten erhält man durch die Trigonometrie.
\[ x=r\cdot cos(\varphi) \] \[ y=r\cdot sin(\varphi) \]Probieren Sie es selber, verschieben Sie den Punkt und beobachten Sie die Berechnung der kartesischen Koordinaten. Rechnen Sie gegebenfalls nach.
Übung 07:
Rechnen Sie die Polarkoordinaten in die kartesischen Koordinaten um: \[ P_1(7\angle15°), \ P_2=(12\angle-35°) \]
Lösung
\[ P_1(6.76, \ 1.81), \ P_2(9.83, \ -6.88) \]
Die kartesischen Koordinaten kann man auch in Polarkoordinaten umrechnen. Dabei ist die Umrechnung für den Radius relativ einfach:
\[ r=\sqrt{x^2+y^2} \]Etwas anspruchsvoller ist die Berechnung des Winkels. Die Berechnung ist nämlich davon abhängig, welche Vorzeichen die kartesischen Koordinaten haben. Man muss die folgende Fallunterscheidung machen:
für x > 0
\[ \varphi =arctan\left(\frac{y}{x}\right) \]für x < 0 und y ≥ 0
\[ \varphi =arctan\left(\frac{y}{x}\right)+90° \]für x < 0 und y < 0
\[ \varphi =arctan\left(\frac{y}{x}\right)-90° \]für x = 0 und y > 0
\[ \varphi =90° \]für x = 0 und y < 0
\[ \varphi =-90° \]Probieren Sie es selber, verschieben Sie den Punkt und beobachten Sie die Berechnung des Winkels. Rechnen Sie gegebenfalls nach.
Übung 08:
Rechnen Sie die Komponenten des kartesischen Koordinatensystems in Polarkoordinaten um: \[ P_1(7, \ 3), \ P_2(-2, \ 9) P_3(-7, \ -3), \ P_4(0, \ 1) \]
Lösung
\[ P_1(7.28 \angle 74.05°), \ P_2(9.22\angle102.53°), P_3=(7.62\angle203.20°), \ P_4(1\angle90°) \]
Aufgaben inkl. Lösungen
Aufgabe 01:
Berechenen Sie den Vektor und die Länge des Vektor \(\overrightarrow{AB}\) aus den folgenden Punkten: \[ a)\quad A=(2,3);\, B=(5,3) \] \[ b)\quad A=(1.2,4);\, B=(5,7.2) \] \[ c)\quad A=(2.3,0);\, B=(-2.5,-3.3) \] \[ d)\quad A=(3.7,-0.5);\, B=(-7.5,2.6) \]
Lösung 01
\[ a)\quad\overrightarrow{AB}=\left(\begin{array}{c}3\\0\end{array}\right)\quad \overline{AB}=1.73\\ \] \[ b)\quad\overrightarrow{AB}=\left(\begin{array}{c}3.8\\3.2\end{array}\right)\quad \overline{AB}=4.97\\ \] \[ c)\quad\overrightarrow{AB}=\left(\begin{array}{c}-4.8\\-3.3\end{array}\right)\quad \overline{AB}=5.82\\ \] \[ d)\quad\overrightarrow{AB}=\left(\begin{array}{c}-11.2\\3.1\end{array}\right)\quad \overline{AB}=11.62\\ \]
Aufgabe 02:
Addieren Sie die folgenden Vektoren. Bestimmen Sie die Lösung durch Zeichnung und Rechnung. \[ a)\quad \vec{a}=\left(\begin{array}{c}-5\\7\end{array}\right), \ \vec{b}=\left(\begin{array}{c}2\\-3\end{array}\right) \] \[ b)\quad \vec{a}=\left(\begin{array}{c}-2\\1\end{array}\right), \ \vec{b}=\left(\begin{array}{c}3\\5\end{array}\right), \ \vec{c}=\left(\begin{array}{c}4\\-2\end{array}\right) \] \[ c)\quad \vec{a}=\left(\begin{array}{c}3\\-1\end{array}\right), \ \vec{b}=\left(\begin{array}{c}2\\1\end{array}\right), \ \vec{c}=\left(\begin{array}{c}6\\-7\end{array}\right), \ \vec{d}=\left(\begin{array}{c}-3\\-2\end{array}\right) \]
Lösung 02
\[ a)\left(\begin{array}{c}-3\\4\end{array}\right) \] \[ b)\left(\begin{array}{c}5\\4\end{array}\right) \] \[ c)\left(\begin{array}{c}8\\-9\end{array}\right) \]
Aufgabe 03:
Berechnen Sie die Vektoren \(\overrightarrow{AB}\), \(\overrightarrow{BC}\), \(\overrightarrow{CD}\) und \(\overrightarrow{AD}\) und stellen Sie es graphisch dar.
\[
A=(-2,-3);\, B=(3,7);\, C=(5,2);\, D=(3,-3)
\]
Welcher Zusammenhang besteht zwischen dem Vektor \(\overrightarrow{AD}\) und den Vektoren \(\overrightarrow{AB}\), \(\overrightarrow{BC}\) und \(\overrightarrow{CD}\)?
Zeigen Sie es mit eine Rechnung.
Lösung 03
\[ \quad\overrightarrow{AB}=\left(\begin{array}{c}5\\10\end{array}\right) \quad\overrightarrow{BC}=\left(\begin{array}{c}2\\-5\end{array}\right) \quad\overrightarrow{CD}=\left(\begin{array}{c}-2\\-5\end{array}\right) \quad\overrightarrow{AD}=\left(\begin{array}{c}5\\0\end{array}\right) \]
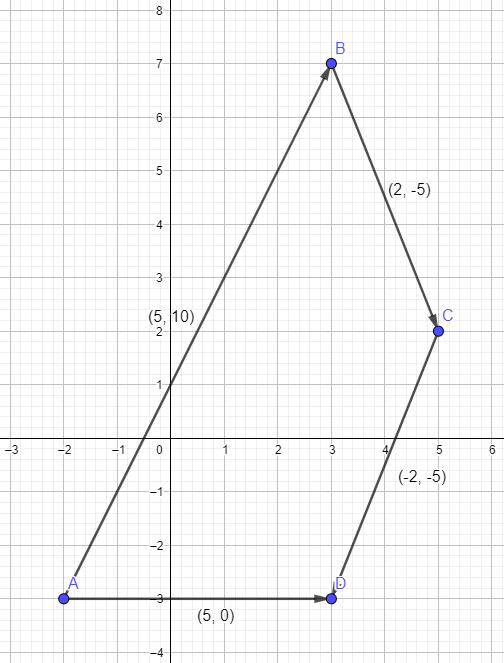
Aufgabe 04:
Addieren Sie die beiden Vektoren vom Ursprung aus und geben Sie Koordinaten des Enpunktes in Polarform an. \[ a)\quad \vec{a}=\left(\begin{array}{c}3\\5\end{array}\right), \ \vec{b}=\left(\begin{array}{c}1\\3\end{array}\right) \] \[ b)\quad \vec{a}=\left(\begin{array}{c}5\\6\end{array}\right), \ \vec{b}=\left(\begin{array}{c}7\\1\end{array}\right) \]
Lösung 04
\[ a) P(4.14\angle-14.28°) \] \[ b) P(5.21\angle33.48°) \]
Aufgabe 05:
Berechnen Sie den Winkel \(\alpha\) der folgenden Dreiecke. \[ a)\quad A=(-2,0);\, B=(3,0);\, C=(0,-5) \] \[ b)\quad A=(2,-1);\, B=(1,0);\, C=(2,-3) \]
Lösung 05
\[ a) \alpha=68.2° \] \[ b)\alpha=135° \]
Aufgabe 06:
Ein Dreieck ABC wird um den Vektor \(\vec{a}\) verschoben. Berechnen Sie die neuen Koordinaten von A, B und C. \[ \quad \vec{a}=\left(\begin{array}{c}-1\\1\end{array}\right);\, A=(2,1);\, B=(7,-1);\, C=(5,5) \]
Lösung 06
\[ A=(1,2);\, B=(6,0);\, C=(4,6) \]
Aufgabe 07:
Ein Dreieck ABC wird im Ursprung um den Winkel \(\alpha\) im Gegenuhrzeigersinn gedreht. Berechnen Sie die neuen Koordinaten des Dreiecks. \[ \quad \alpha = 30°;\, A=(-1,3);\, B=(2,4);\, C=(3,2) \]
Lösung 07
\[ A=(-2.37,2.10);\, B=(1.60,3.23);\, C=(-0.27,4.46) \]
Physik Pilotaufgaben
Lösen Sie die folgenden Physikaufgaben mit der Theorie der Vektoren und der Polarkoordinaten.
Sie können die Aufgaben auch als PDF herunterladen: IDAF_Physikaufgaben.pdf
Pilotaufgabe 01:
An einem Telephonmast ziehen drei Drähte nach den gegebenen Richtungen.
Gegeben:
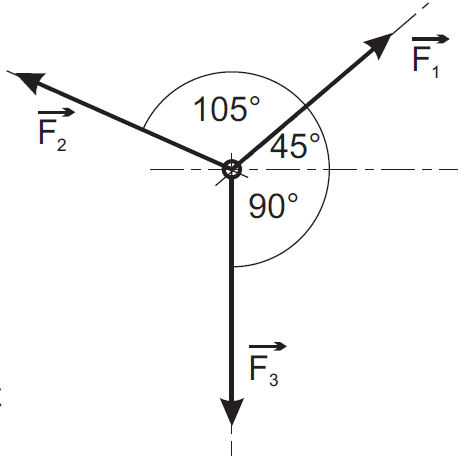
\[
F_1=400\ N
\]
\[
F_2=600\ N
\]
\[
F_3=450\ N
\]
Gesucht:
a) Zeichnen Sie den Kräfteplan massstäblich!
b) Wie gross ist die Summenkraft \(F_s\) auf den Mast?
c) Wie gross ist der Winkel zwischen \(F_1\) und \(F_s\)?
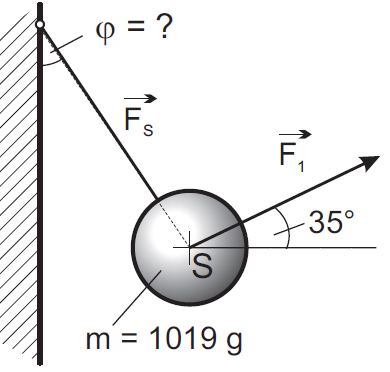
Pilotaufgabe 02:
Eine Stahlkugel mit der Masse \(m = 1019\ g\) hängt gemäss Skizze an einem Seil an der Wand.
Sie ziehen mit einer Kraft \(F=4\ N\) unter einem Winkel \(\alpha=35°\) zur
Horizontalen nach oben. Es stellt sich ein statisches Gleichgewicht ein.
Gegeben:
Gesucht:
a) Erstellen Sie einen Lageplan!
b) Erstellen Sie einen massstäblichen Kräfteplan!
c) Wie gross ist die Kraft F im Seil?
d) Wie gross ist der Winkel zwischen Wand und Seil?
Pilotaufgabe 03:
Eine Ampel mit der Masse \(12\ kg\) ist über einer Strasse zwischen
zwei Hauswänden gemäss unten stehender Abb. aufgehängt.
Gegeben:

Gesucht:
Wie gross sind die Kräfte in den beiden Seilen?